lunes, 16 de diciembre de 2013

Calificaciones finales del examen de matematicas.


Carrera: Informatica C-V			Carrera: REFRIGERACION			Carrera: MECANICA

NUMERO	CALIFICACION	30%	NUMERO	CALIFICACION	30%	NUMERO	CALIFICACION	30%
1	76	22.8	1	65	19.5	1	46	13.8
2	60	18	2	16	4.8	2	35	10.5
3	75	22.5	3	55	16.5	3	25	7.5
4	85	25.5	4	75	22.5	4	16	4.8
5	20	6	5	26	7.8	5	70	21
6	75	22.5	6	31	9.3	6	52	15.6
7	45	13.5	7	17	5.1	7	47	14.1
8	70	21	8	52	15.6	8	44	13.2
9	75	22.5	9	0	0	9	36	10.8
10	70	21	10	37	11.1	10	22	6.6
11	80	24	11	44	13.2	11	21	6.3
12	85	25.5	12	76	22.8	12	25	7.5
13	65	19.5	13	67	20.1	13	37	11.1
14	15	4.5	14	71	21.3	14	27	8.1
15	100	30	15	24	7.2	15	46	13.8
16	35	10.5	16	32	9.6	16	22	6.6
17	40	12	17	49	14.7	17	40	12
18	40	12	18	70	21	18	37	11.1
19	80	24	19	71	21.3	19	90	27
20	55	16.5	20	62	18.6	20	52	15.6
21	60	18	21	48	14.4	21	44	13.2
22	65	19.5	22		0	22	47	14.1
23	98	29.4	23		0	23	40	12
24	50	15	24		0	24		0

domingo, 15 de diciembre de 2013

Funciones trigonométricas

En matemáticas, las funciones trigonométricas son las funciones establecidas con el fin de extender la definición de las razones trigonométricas a todos los números reales y complejos. Las funciones trigonométricas son de gran importancia en física, astronomía, cartografía, náutica, telecomunicaciones, la representación de fenómenos periódicos, y otras muchas aplicaciones.

Las Razones trigonométricas se definen comúnmente como el cociente entre dos lados de un triángulo rectángulo asociado a sus ángulos. Las funciones trigonométricas son funciones cuyos valores son extensiones del concepto de razón trigonométrica en un triángulo rectángulo trazado en una circunferencia unitaria (de radio unidad). Definiciones más modernas las describen como series infinitas o como la solución de ciertas ecuaciones diferenciales, permitiendo su extensión a valores positivos y negativos, e incluso a números complejos.

Existen seis funciones trigonométricas básicas. Las últimas cuatro, se definen en relación de las dos primeras funciones, aunque se pueden definir geométricamente o por medio de sus relaciones. Algunas funciones fueron comunes antiguamente, y aparecen en las primeras tablas, pero no se utilizan actualmente; por ejemplo el verseno (1 − cos θ) y la exsecante (sec θ − 1).

Función	Abreviatura	Equivalencias (en radianes)
Seno	sin (sen)	$\sin \; \theta \equiv \frac{1}{\csc \theta} \equiv \cos \left(\frac{\pi}{2} - \theta \right) \equiv \frac{\cos \theta}{\cot \theta} \,$
Coseno	cos	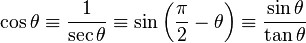$\cos \theta \equiv \frac{1}{\sec \theta} \equiv \sin \left(\frac{\pi}{2} - \theta \right) \equiv \frac{\sin \theta}{\tan \theta} \,$
Tangente	tan	$\tan \theta \equiv \frac{1}{\cot \theta} \equiv \cot \left(\frac{\pi}{2} - \theta \right) \equiv \frac{\sin \theta}{\cos \theta} \,$
Cotangente	ctg (cot)	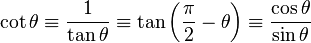$\cot \theta \equiv \frac{1}{\tan \theta} \equiv \tan \left(\frac{\pi}{2} - \theta \right) \equiv \frac{\cos \theta}{\sin \theta} \,$
Secante	sec	$\sec \theta \equiv \frac{1}{\cos \theta} \equiv \csc \left(\frac{\pi}{2} - \theta \right) \equiv \frac{\tan \theta}{\sin \theta} \,$
Cosecante	csc (cosec)	$\csc \theta \equiv \frac{1}{\sin \theta} \equiv \sec \left(\frac{\pi}{2} - \theta \right) \equiv \frac{\cot \theta}{\cos \theta} \,$

Definiciones respecto de un triángulo rectángulo

Para definir las razones trigonométricas del ángulo: $\alpha$ , del vértice A, se parte de un triángulo rectángulo arbitrario que contiene a este ángulo. El nombre de los lados de este triángulo rectángulo que se usará en los sucesivo será:

La hipotenusa (h) es el lado opuesto al ángulo recto, o lado de mayor longitud del triángulo rectángulo.
El cateto opuesto (a) es el lado opuesto al ángulo $\alpha$ .
El cateto adyacente (b) es el lado adyacente al ángulo $\alpha$ .

Todos los triángulos considerados se encuentran en el Plano Euclidiano, por lo que la suma de sus ángulos internos es igual a πradianes (o 180°). En consecuencia, en cualquier triángulo rectángulo los ángulos no rectos se encuentran entre 0 y π/2 radianes. Las definiciones que se dan a continuación definen estrictamente las funciones trigonométricas para ángulos dentro de ese rango:

1) El seno de un ángulo es la relación entre la longitud del cateto opuesto y la longitud de la hipotenusa:

$\sin \alpha = \frac {{ \color{ForestGreen}\textrm{opuesto}}} {{ \color{Red}\textrm{hipotenusa}}} = \frac {a} {h}.$

El valor de esta relación no depende del tamaño del triángulo rectángulo que elijamos, siempre que tenga el mismo ángulo $\alpha$ , en cuyo caso se trata de triángulos semejantes.

2) El coseno de un ángulo es la relación entre la longitud del cateto adyacente y la longitud de la hipotenusa:

$\cos \alpha = \frac {{ \color{Blue}\textrm{adyacente}}} {{ \color{Red}\textrm{hipotenusa}}} = \frac {b} {h}.$

3) La tangente de un ángulo es la relación entre la longitud del cateto opuesto y la del adyacente:

$\tan \alpha = \frac {{ \color{ForestGreen}\textrm{opuesto}}} {{ \color{Blue}\textrm{adyacente}}} = \frac {a} {b}.$

4) La cotangente de un ángulo es la relación entre la longitud del cateto adyacente y la del opuesto:

$\cot \alpha = \frac {{ \color{Blue}\textrm{adyacente}}} {{ \color{ForestGreen}\textrm{opuesto}}} = \frac {b} {a}.$

5) La secante de un ángulo es la relación entre la longitud de la hipotenusa y la longitud del cateto adyacente:

$\sec \alpha = \frac {{ \color{Red}\textrm{hipotenusa}}} {{ \color{Blue}\textrm{adyacente}}} = \frac {h} {b}.$

6) La cosecante de un ángulo es la relación entre la longitud de la hipotenusa y la longitud del cateto opuesto:

$\csc \alpha = \frac {{ \color{Red}\textrm{hipotenusa}}} {{ \color{ForestGreen}\textrm{opuesto}}} = \frac {h} {a}.$

Funciones trigonométricas de ángulos notables

	0°	30°	45°	60°	90°
sen	0	$\frac{1}{2}$	$\frac{\sqrt{2}}{2}$	$\frac{\sqrt{3}}{2}$	1
cos	1	$\frac{\sqrt{3}}{2}$	$\frac{\sqrt{2}}{2}$	$\frac{1}{2}$	0
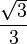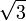tan	0	$\frac{\sqrt{3}}{3}$	1	$\sqrt{3}$	$\infty$

domingo, 10 de noviembre de 2013

Reflexiones para un amig@

Escuchenla bien y pongalan en practica siempre...

sábado, 2 de noviembre de 2013

La antigua Grecia

martes, 22 de octubre de 2013

Reflexiones para un amig@

By: Sugery Bueno.

lunes, 21 de octubre de 2013

Fecha limite de entrega de Practicas

En vista de la suspensión de docencia la fecha limite para entregar las practicas correspondientes a los números complejos será el lunes 28 de octubre cada vicepresidente (o secretario) del curso sera el responsable de recolectarlas en su curso y entregármelas en mis manos.
nota: no habrá prorroga quien no la entregue ese día pierde los 20 pts.

jueves, 17 de octubre de 2013

Reflexion para un amig@

martes, 15 de octubre de 2013

Transformaciones Geomètricas

sábado, 12 de octubre de 2013

Próximo Tema: Unidad II Transformaciones Geométricas

Geometria de las transformaciones pag. 320 libro de matemática de 4to grado Rafael Peña.

Estudiar los conceptos basicos y realizar anotaciones para participar en clase la próxima semana.

Practica para los Estudiantes de 4to grado , Informatica, Refrigeracion y Mecánica 2013-2014

Politécnico Vicente Aquilino Santos

Práctica sobre los números complejos.

(fecha de entrega: viernes 25 de Octubre. Valor 20 pts.)

Comprueba lo aprendido

Ø Realiza 5 operaciones de sumas de números complejos.

Ø Realiza 5 operaciones de restas de números complejos.

Ø Realiza 5 operaciones de multiplicación de números complejos.

Ø Realiza 5 operaciones de division de números complejos.

Ø Realiza 5 operaciones de potencias de números complejos

(3 elevadas al cuadrado y dos al cubo).

Ej: (3 + 2i) (-5+ 4i) , (6 - 2i) – (3 + 4i)…

Nota: debe haber por lo menos un número negative en cada operación. Ademas cada quien debe de construir sus propios ejercicios. Todas las prácticas que sean iguales se anulan.